这篇文章是受到 StackOverflow 上这个帖子和这篇博客的启发，我讨论了下 HTML + CSS 是否图灵完备和几个例子。我会简单介绍下文中需要用到的概念，已经懂的部分就跳过，不懂的可能还是得多 google。

背景知识

HTML

HTML 就是拿来排版网页的语言，语法很容易，举几个例子。

<HTML>
<body>
  <h2>My First Heading</h2>
  <p>My first paragraph.</p>
</body>
</HTML>

这段代码就会生成一个这样的页面，

My First Heading

My first paragraph.

元素 <h2> 指的是标题，<p> 指的是段落。HTML 有各种各样的元素，下面是个复选框 (checkbox) 元素，

<HTML>
<body>
  <form>
     <p><input type="checkbox" name="vehicle" value="Bike" /> I have a bike</p>
     <p><input type="checkbox" name="vehicle" value="Car"/> I have a car</p>
     <input type="submit" value="Submit" />
  </form>
</body>
</HTML>

就会生成这样一个大家常见的复选框，

I have a bike

I have a car

这里要强调的是复选框是有状态的，状态可以是 checked 或者 unchecked。这点在后面会反复用到。HTML 还可以对任意元素赋予类 (class) 和 id，比如这样，

<HTML>
<body>
  <h2 class="foo">My First Heading</h2>
  <p id="bar">My first paragraph.</p>
  <p class="foo" id=”p2”>My second paragraph.</p>
</body>
</HTML>

这里 <h2> 和第二个 <p> 就被放到了 “foo” 类下，而两个 <p> 则各自有了 id 名。不同元素可以有同一个类名，但id必须是独特的。加上类名和 id 并不会改变页面显示效果，但可以标记元素方便查找修改。这在 CSS 部分会具体解释。

CSS

HTML 元素提供了基本的样式，但你还可以进一步定义，最直接的办法是在元素里使用 style 属性，比如对上面第一段程序略作修改，

<HTML>
<body>
  <h2 style="color:red">My First Heading</h2>
  <p style="font-size:30px">My first paragraph.</p>
</body>
</HTML>

效果就会变成这样，

My First Heading

My first paragraph.

但这显然很繁琐，如果我想让所有 <p> 元素都是30号字难道要一个个标签改过去吗。CSS 就提供了全局控制 HTML 样式的方法。你在一个 CSS 文件里写下

p {color: red}

然后让你想改变的 HTML 文件读入这个 CSS，所有的段落就都会变成红色了。这里的 p 就是一个选择器，它选中了所有的 <p> 标签。CSS 里还有很多其他的选择器，供你对要修改的地方进行精确定位，比如

.foo {color:red}

就会选中 class 名为 foo 的元素进行操作（上节中的 <h2> 和第二个 <p>)，而

p.foo

就只会选中 foo 类里的 <p> 元素，而不会选中 <h2>。id 的选择是类似的，不过是变成以#开头而已。

#bar

就会选中上节第一个 <p>。还可以利用状态来进行选择，在上节复选框的例子中，

input:checked

就会选中被勾选的复选框，因为是否勾选是用户手动决定的，这个选择器就可以让你动态的改变样式（比如被勾选中时字就变红）。 还有一个叫兄弟选择器的，利用加号来表示某个元素的下一个元素，比如

h2 + p {color: red}

表示如果某个 <h2> 紧接的下一个元素是 <p>，则这个 <p> 会被变成红色。类似的，

p.foo + * + * {color: red}

则会把属于foo类的所有 <p> 元素往后数的第二个元素变成红色（因为星号会匹配任意元素）。如果把加号改成波浪号~，则会放宽标准，不再要求紧跟，而是只要在之后出现就会被选中。注意 CSS 中不存在选中某元素之前元素的选择器，所以我觉得其实更应该叫“弟弟选择器”而不是“兄弟选择器” 。。这个选择器后文会反复使用。

单带图灵机

这个大家应该都略有所知，就是一条纸带一个读写头然后在那挪来挪去，纸带上写着0或1或空白 (b)，读写头可以读、写（废话）并具有一个状态，像这样：

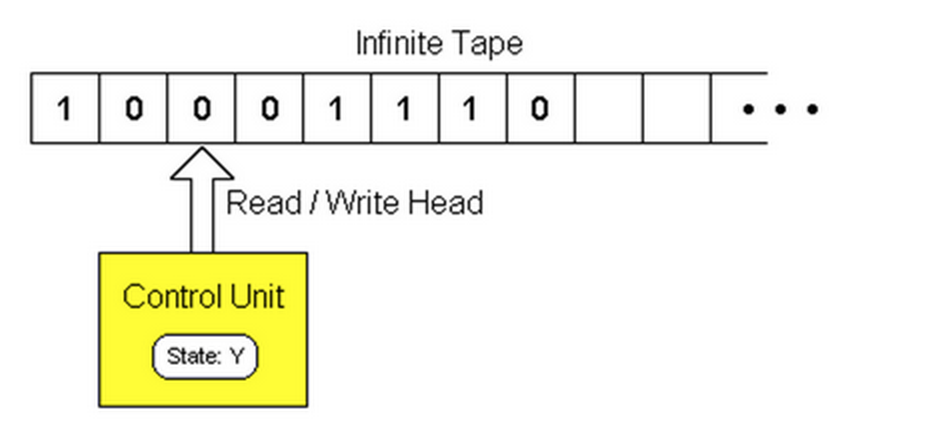
turing machine

但具体是怎么运算的呢？很简单，每个程序由一个状态表构成，这篇文章给了两个简单的例子，这是一个f(x) = x + 1 的程序：

q1, 0, 1, l, q2;
q1, 1, , 0, l, q3;
q1, b, b, n, q4;
q2, 0, 0, l, q2;
q2, 1, 1, l, q2;
q2, b, b, n, q4;
q3, 0, 1, l, q2;
q3, 1, 0, l, q3;
q3, b, b, n, q4.

五元组 (q1, s1, s2, r, q2) 分别表示：

  • q1: 当前状态
  • s1: 读写头从当前读入的数据（0或者1）
  • s2: 读写头即将写入当前方格的数据
  • r/l/n: 读写头向右移动一格/向左移动一格/保持不动
  • q2: 新状态

看着有点复杂，我举个例子，读写头初始总是指向纸带的最右边（最低位）并且状态为 q1，如果纸带上一开始写着10（其余格子都写着b），读写头就是先指着0，因为状态为 q1，我们就去找状态表中以 q1, 0开头的那行，就是第一行，第一行的后三个值是1，l，q2，意思依次是：第一步完成后，把个位的0改写成1；读写头左移一位（现在指向十位的1了），把读写头的状态改成 q2。第二步类似，找到 q2, 1开头的那行（第五行），它给出的操作是写入1（也就是没变），左移一格，状态为 q2。现在读写头指向 b 了，于是第三步就该按 q2, b, b, n, q4 来了，纸带值不变，读写头也不动，状态被改为 q4，而 q4 的意思是结束。所以程序运行完了。现在纸带上留下了11，跟输入的10相比加了1，类似的你可以分析输入11输入11时的情况，你会发现要用到状态 q3，而这里 q3 其实是用来表示需要进位。

文中还给了 f(x) = 2^x 的状态表，此处不赘，只提下思想：“我们知道，在二进制表示下，只要在原数后面添上一个0，就是原来的数乘以二。根据这个思想，我们每次在原数后面写一个0，同时原数减一，直到原数减为0，再在所写的0前面添加上一个1，就能得出所求函数的答案了。”

请确保你至少看懂了加一函数的原理再往下。

图灵完备

图灵证明有了这个简陋的纸带+读写头设备就能够运行一切可计算的程序，而任何能够模拟单带图灵机（也因此能运行一切可算的程序）的东西就被称作是图灵完备的。我们常见的所有编程语言都是图灵完备的，但有些看着奇奇怪怪的东西其实也是图灵完备的，比如某些元胞自动机。

元胞自动机

二维

元胞自动机里最著名的一个例子大概就是康威生命游戏了。规则是这样的，在一个无穷大的二维网格上，对于每个格子，可以有两种状态-存活或死亡，每个格子与以自身为中心的周围八个格子产生互动。

  • 当前格子为存活状态时，当周围低于2个（不包含2个）存活格子时， 该格子变成死亡状态。（模拟生命数量稀少）
  • 当前格子为存活状态时，当周围有2个或3个存活格子时， 该格子保持原样。
  • 当前格子为存活状态时，当周围有3个以上的存活格子时，该格子变成死亡状态。（模拟生命数量过多）
  • 当前格子为死亡状态时，当周围有3个存活格子时，该格子变成存活状态。 （模拟繁殖）

没懂的去看下维基的图就懂了，很简单。重要的是这套规则下的生命游戏已经被证明是图灵完备的了。

康威生命游戏中存在一些简单的模式，还是请自己点开链接看，我这里只讲一个叫做glider的，长这样

glider gif

在这套生命游戏的规则下，这组格子会不断的变回自身并一直朝一个方向移动，此类模式因此被叫做 spaceship，glider 是其中最简单的一个。glider 的这个状态 hacker emblem 被 Eric Raymond 提议作为黑客的标志并被广泛接受，不过二维元胞自动机与本文并无直接关系。。我讲一下是为了强调它在黑客文化里的重要性。

一维

一维的情况就更简单了，一条纸带上，每个格子的下一个状态由左右两格和它自己的值（也就是一个三位数）决定，而二进制下三位数总共就8个，每个都可以映射到0或1，所以总共只有2^8 = 256种规则，下面是其中一种：

当前状态 111 110 101 100 011 010 001 000
新状态 0 1 1 0 1 1 1 0

因为二进制01101110（上表第二行）是十进制下的110，所以这个规则定义的元胞自动机就被称作 Rule 110，类似的我们有 Rule 0 到 Rule 255。Rule 110 也被证明是图灵完备的。

HTML / CSS的图灵完备性

在为了自洽讲了那么多基础概念后，我们终于能讲正题了：HTML / CSS是图灵完备的吗？

你把 HTML 跟其他”正常“的编程语言比一下就知道它有多简陋了，HTML 里你不能声明变量（没有 x = 2 这种东西），不能写循环，也没有 if...else 这种条件判断语句。它看着就是个告诉浏览器这段话是标题，用24号字，那段话用蓝色，这里用宋体……的排版工具，当前端开发人员需要些程序性的东西的时候，他们会用 JavaScript，有时你还会看到有人问“前端真的算编程吗”之类的。所以当我一搜 ”HTML 图灵完备“出来的页面都告诉我它不是图灵完备时我一点也不意外，直到我看到了文章开头提到的那个 StackOverflow 上的帖子。在这个帖子里有人只用 HTML + CSS写出了 Rule 110（大家在电脑上自己玩下），而我们已经知道 Rule 110是图灵完备的了。我的第一反应当然是虎躯一震 (ﾟдﾟ≡ﾟдﾟ)，但事后想想虽然 HTML 没这没那，单带图灵机不也啥都没有吗。那你肯定还是会好奇，具体到底是怎样实现的？让我们看看代码吧（这个代码只支持基于 webkit 的浏览器，听不懂的你用 Chrome 就对了），这里的关键有两处。

首先创建一大堆的复选框，

<!-- A total of 900 checkboxes required -->
<input type="checkbox" />
<input type="checkbox" />
<input type="checkbox" />
<input type="checkbox" />
<input type="checkbox" />
<input type="checkbox" />
<input type="checkbox" />
<input type="checkbox" />
<input type="checkbox" />
...

从而得到一个二维网格:

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

...

网格的第一行用户可以自定义输入的数字，之后第二行就是第一行按 Rule 110 演化一次的结果，第三行就是第二行演化一次的结果……。这里的演化是通过此类代码实现的：

input:checked +
    *+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+*+
    input::before {
content: "1";
}

大致意思是：如果一个格子被选中 (checked) 了，往后数第三十个元素，如果也是 <input> 类型，把它改写成1。这里用到了前面基础部分强调的两个东西，一是复选框是有状态的，所以我们可以利用 input:checked 来进行查询，第二是利用兄弟选择器来找到其后第三十个元素来操作，而上一步生成的二维网格每一行有30个格子，所以这里就是在根据一个格子的值去操作它下一行相应位置的值。剩下的工作就是把 Rule 110 的所有规则都以这种方式放进去就是了。

总结下，复选框提供了一个布尔值，而我们可以声明无限的复选框，所以其实可以表示出任意的数/状态，这变相克服了 HTML / CSS 不能声明变量的问题；兄弟选择器则提供了一种模式匹配，实现了 if...else 的部分功能，说”部分“是因为它只能往后操作，不能向前（果然还是该叫“弟弟选择器”）。这个单向性在后面还会详细讨论。

扫雷

文章开头提到的另一个帖子借鉴了这个思路，写了一个纯 HTML / CSS实现的扫雷。做法非常类似，不过这里声明的复选框被分成了两块，但这没有本质区别。

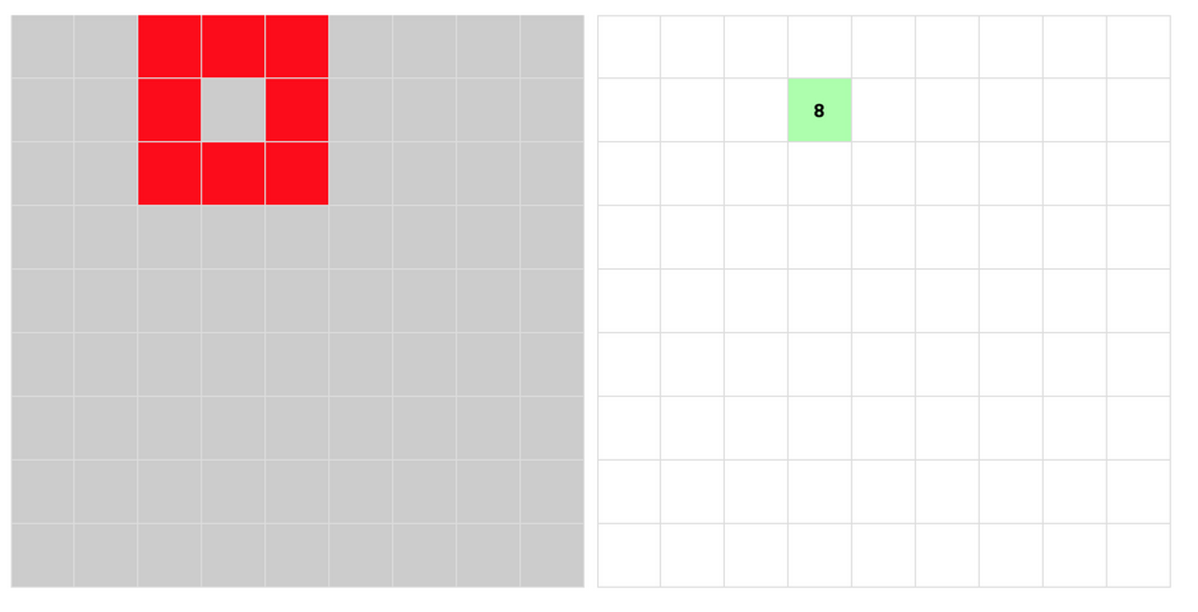
minesweeper1

然后利用兄弟选择器，比如若想要匹配上图的情况，就是去找到连续三个 checked，而且往后数一行又找到两个 checked 中间夹一个 unchecked，而且再数一行又找到三个连续 checked，然后再一路狂数到右边部分如果正好图中绿色位置也被点开 (checked)，就在那里显示8。如果你反应快的话，可能会意识到这在边界处可能有 bug，因为所谓的下一行其实是我们看到的，程序里完全是通过数个数来定位“下一行”的，所以下图这样的情况似乎也会给出8。

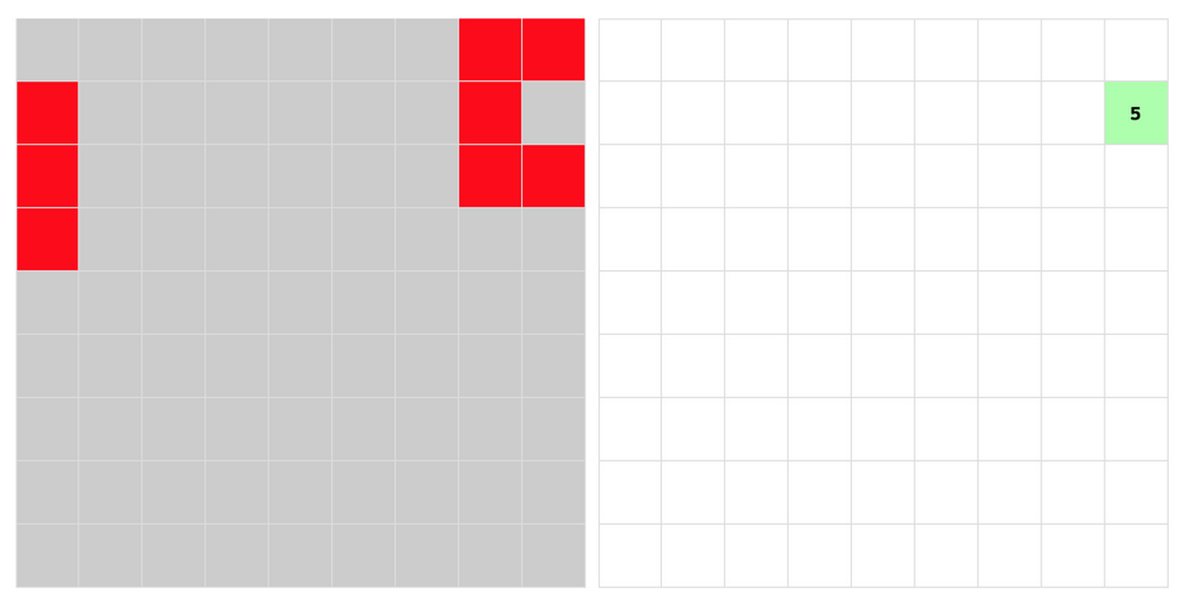
minesweeper2

当然实际上并没有，因为作者在每行后面加入了两个不显示的复选框，起到了类似换行符的作用，所以灰色区域在程序看来是9×11的网格。每行后面两个不显示从而也无法被选中的格子保证了如果有连续三个 checked，那一定是在同一行。

加一器

看到这么酷酷的思路我当然也按捺不住了，所以我决定站在前人的肩膀上，写个比他们都简单的程序( ͡° ͜ʖ ͡°)。恩就决定是你了，单带图灵机的加一程序：GitHub地址、项目页面（得在电脑上打开，建议 Chrome）。效果是这样滴，

increment by one function

你在第一行表示好你想要的输入数字，右上角点开始后就 tab，空格一直交替按，第二行就会给出第一行+1的数了。第三行表示是否需要进位，第四行表示这位是否处理完了。 这个程序的小创新在于显式地使用了状态/分隔符，也就是第三行和第四行。引入它们是为了克服 CSS 的全局性。比如你要把个位加一，于是在 CSS 里面定义了只要第一格是0第二格就写成1，而除了个位之外其他还保留原样。这显然不行，因为可能会需要进位，这看起来也不会有单带图灵机里一位一位处理的效果。而引入状态符后，通过给每行的格子不同的类名，我就可以这样写，

/*Process other digits*/
input.processed:checked +*+*+*+*+*+*+*+*+*+ input.processed{
    display: block;
}

input.carrying:checked +*+ input.processed:checked +*+*+*+ input.inp:not(:checked) +*+ input.out{
    display: block;
}

input.carrying:checked +*+ input.processed:checked +*+*+*+ input.inp:checked +*+*+*+ input.carrying{
    display: block;
}

input.carrying:not(:checked) +*+ input.processed:checked +*+*+*+ input.inp:checked +*+ input.out{
    display: block;
}

首先这里与前面讨论的 Rule 110 代码有个小不同，就是我不是直接往格子里写1，而是把想要写1的格子显示出来，这样你在按 tab 键的时候它们就会挨个被聚焦，然后你按空格就会选中（这就是你得 tab、空格不停交替按的原因）。其实 Rule 110 也是这样写的，不过那帖子里给了一个项目页面，一个 JsFiddle 的源码，我上面详细讨论的是后者，而这里的写法是从前者那借(chao)鉴(xi)的。

其次你可以看到我利用 input.processed:checked 来定位待处理的数位，那些还没处理到的数位它们的 input.processed 是 unchecked 的，所以不会被匹配，这就保证了类似单带图灵机的局部、动态效果。

零磁场下匀相互作用二维伊辛模型的蒙特卡洛模拟

这标题估计直接撂倒一片。不过因为我并没最终做出来，所以就不详细解释了。伊辛模型是统计/相变物理中最基础而重要的模型之一（杨振宁职业生涯的一项重要成果就与之有关），但解析行为并不易得，简单做法就是用蒙特卡洛模拟，分五步：

  1. Pick a spin site using selection probability g(μ, ν) and calculate the contribution to the energy involving this spin.
  2. Flip the value of the spin and calculate the new contribution.
  3. If the new energy is less, keep the flipped value.
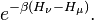  4. If the new energy is more, only keep with probability e^{-\beta(H_\nu-H_\mu)}..
  5. Repeat.

我最开始是想写这个的，但发现太难了。

第一步生成 g(μ, ν) 就是个困难，不过可以不管，我们就按顺序一个个格子去变，模拟的足够久就不会影响结果。

第二步计算能量很简单，如果我们把相邻格子定义为周围八个格子的话，就跟扫雷几乎一样，去数下有几个格子和中心格同值就行。而第三步在扫雷语境下就是：如果中心格子不是雷，那你点开它显示的雷数如果小于5，就不变，反之亦然。第五步当然也不会有问题。

问题出在第四步，你可能觉得怎么可能用 CSS 算出指数函数（玻尔兹曼因子），但这其实也可以绕过，因为在给定温度下，如果假设周期性边界条件，这里的玻尔兹曼因子总共就可能取四个值，事先手算好就行。难是难在怎么生成一个随机数并与玻尔兹曼因子比较。HTML / CSS 没有内置的随机数生成器，而靠着 Rule 110 写一个大概是不可能的吧。。我能想到的可能的方式是读取例如当前系统时间的毫秒位或者cpu温度之类随机的物理量来产生随机数，但也没找到此类函数。而得到随机数后与玻尔兹曼因子比大小我也还没想出办法，不过这个也许容易点，不难想象用类似加一器的写法去写个单独的比较器，把两个数从高位到低位进行比较，只是要把它嵌入到蒙特卡洛里也许就要费一番功夫了。

我把这半成品放在这是因为对 HTML / CSS 我还很新手（刚学一礼拜），可能有我还没想到的巧妙方法可以绕过这些困难，如果激发了哪位高手的灵感还望留言讨论。

讨论

HTML / CSS是图灵完备的吗？

你可能会说我怎么这么啰嗦，上面不都讲了那么多遍了吗(╯‵□′)╯︵┻━┻。

但你仔细看下 StackOverflow 那帖子里的讨论就会发现没这么简单，这个 Rule 110 实现是需要用户不断交替地按 tab 和空格键的。所以在扫雷作者的博文里他就认为这不是真的图灵机，只是个手动机，根本不是什么元胞“自动”机，也就跟个有限状态机差不多。

但这是错的。SO 原帖讨论里也有人指出了，即使是单带图灵机，也是需要机械设备支持的，没有些连杆齿轮之类的怎么让纸带和读写头移来移去？只是我们平时没去考虑而已。这个 HTML / CSS 手动机需要的也只是个机械地按 tab 和空格键的外设，这并不影响其图灵完备性。

有限状态机 vs. 图灵机

HTML / CSS 毫无疑问是可以实现有限状态机的（毕竟都图灵完备了）。我们看看加一器吧，比如你要对任意两位数实现加一，除了我的通用写法外，有限状态机方式的实现无比简单，你就穷举所有的二进制两位数（就四个）和他们的相应操作就行了，比如

input:checked + input:unchecked + 对output部分的某些操作

就是在对10进行处理。它与图灵机的区别就是它就只能处理这四个数（所以叫有限状态），而图灵机的纸带可能是无限长的。当你想把这个加一器用到三位数上时，你就得增加穷举。但反正它永远也处理不了无限长的纸带。

这里的关键就在于是否能将穷举分类为有限的匹配模式。当穷举得对输入进行整个的匹配，那你就只能从头穷举到尾，自然也就不可能处理无限长的情况。而如果可以将无限的穷举空间划分为有限的匹配模式，那就可以找到通解，而这意味着必然有些匹配模式是局域的，例如上文中的找到三个连续的 checked。它们可以在任意位置，前后也可以有各种情况。这种“短视”的视野在面对无穷时反而成了优势。

复选框=内存，兄弟选择器操作读写头

现在我们把此类 HTML / CSS 图灵机与其他图灵机比较一下。不难发现复选框起的作用就是输入设备+内存，你在复选框串的前部写入，而后利用各种选择器（主要是兄弟选择器）来移动读写头到复选框串的后部的相应位置进行操作。而类名则可以当做一个打包工具，比如我把十个复选框放到一个类里，先使用类名选择器，再用兄弟选择器，我就可以十分容易地访问这十个元素，这其实不就是个数组了吗？id 名则可以用来划分和定位内存，比如某个 id 左边是输入，右边是输出之类的。

这样一看似乎常见的程序功能我们都齐备了，现在就像正常程序那样拿来玩就好啦。但并没有，这里有个重要区别，就是它只有弟弟选择器而没有哥哥选择器啊(／‵Д′)／~ ╧╧。这意味着这内存是只能利用上游元素来操作下游元素而不能反过来的。当然因为我们已经证明它是图灵完备的了，所以任何程序你都总能绕路写出来，我们来看看怎么绕比较方便吧。

单向内存下的程序设计

我们现在看个稍微复杂点的函数，单带图灵机那节里的 f(x) = 2^x 函数。先重温下思想："我们知道，在二进制表示下，只要在原数后面添上一个0，就是原来的数乘以2。根据这个思想，我们每次在原数后面写一个0，同时原数减一，直到原数减为0，再在所写的0前面添加上一个1，就能得出所求函数的答案了。"

用HTML / CSS该怎么写？

我并没有真的写，但想了下下图这样似乎可以实现。

tail recursion in single tape Turing machine

每个迭代函数需要记录两个量，一个不断减一的输入和一个依次加零的输出。当某步的输入区为零时就选中返回标记，当返回标记被选中就会去写结果区从而停机。

而这不就是尾递归吗？

普通递归与尾递归

要介绍尾递归，我们先来看个使用递归的最简单例子，求阶乘。直接的递归写法是这样的： 

def f(n):
  if n == 0:
    return 1
  else:
    return n*f(n-1)

当你求6的阶乘时，它算到 return 那里，发现需要计算6 * f(5)，于是开一块新的内存区去算 f(5)，而要算 f(5) 又要先算出5 * f(4)，于是又开一块内存，到最后再一个个回头，如下图。

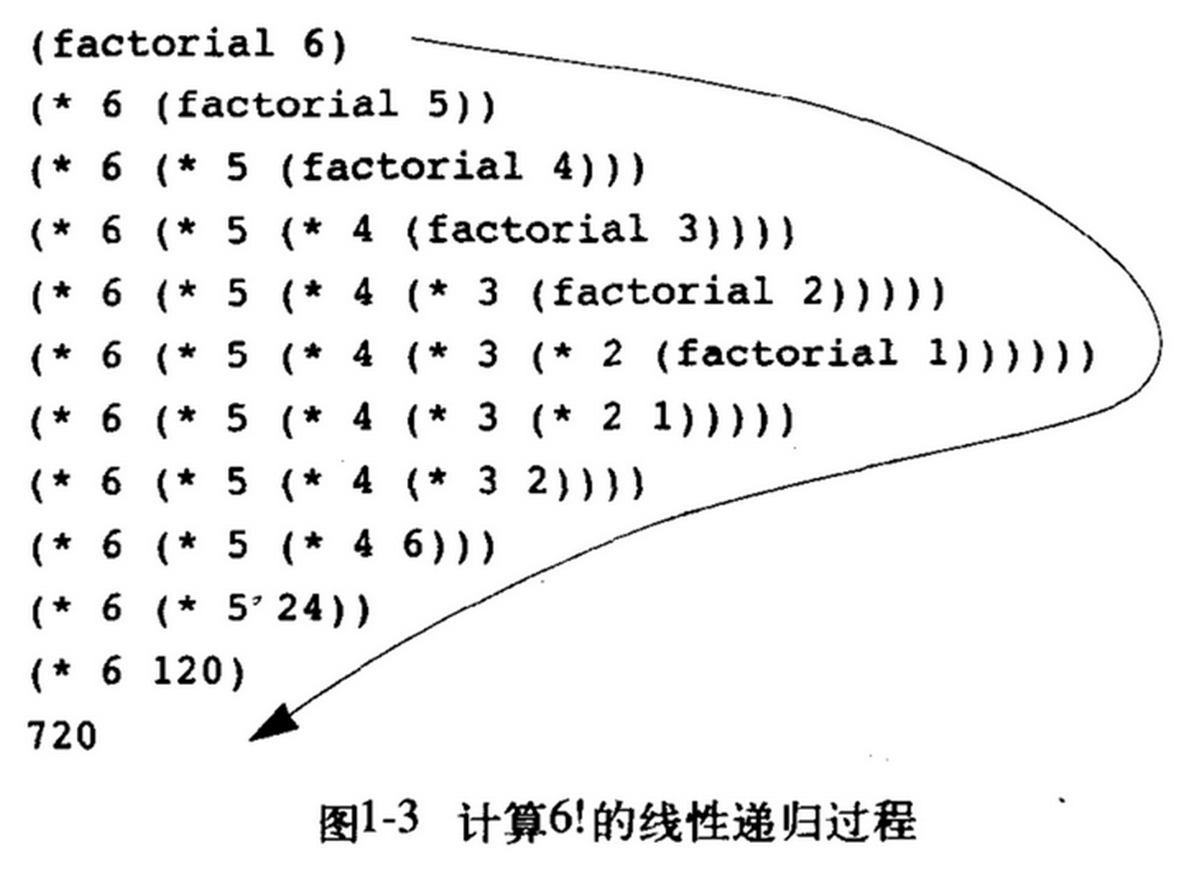
normal recursion in memory

而尾递归写法是这样的：

def f(n, result=1):
  if n == 0:
    return result
  else:
    return f(n-1, n*result)

这时候算 f(6) 是这样的，f(6) 就等于 f(5, 6*1) = f(4, 6*5) = f(3, 6*5*4) = …… = f(0, 6!) = 6!。这不也是递归吗，看着还更复杂，有什么好的？好处就是它每一步的返回值都不需要再运算，直接等于你最终要的结果，所以中间调用完全无需保留，你调用完 f(5) 你就可以把它的内存释放安心去算 f(4, 6*5) 了，所有你关心的信息都不会丢失，所以它的内存调用是这样的：

tail recursion in memory

栈空间的要求是 O(1)，比起递归那种分分钟爆栈的写法要好得多。当然这种性能上的提升要求编译器懂得在遇到尾递归的时候去释放中间调用的空间，这在函数式语言的编译器里常见，但大家比较熟悉的编程语言 (C, Python…)一般是没对尾递归做这种优化的，所以它们依然会开着那些内存等着返回值，与普通递归在性能上没有区别。

但内存占用完全不是我们这里的关注点，都在用 CSS 写图灵机了谁还关心性能。。这里的重点在于图上的箭头，普通递归的内存读写头需要双向移动，而尾递归则只要一个方向，这就正好符合我们的需要。上面图示里的迭代处理区每一步都包含中间输出也就不奇怪了，这保证了我们可以一路向右永不回头。

最后我们看一下另一个常见的流程控制：循环。回到本节开始时的 f(x) = 2^x 函数，尾递归这样写：

init = 1
def f(x, result):
  if x == 0:
    return result
  else:
    return f(x-1, 10*result)

print f(n, init)

循环这样写:

result = 1
for i in range(n):
  result = 10 * result
print result

对应到复选框构成的内存上你大概需要这样操作：

loop in single tape Turing machine

你可以看出这和尾递归的流程极其相似，每个中间过程都保存一个中间结果，这个结果在最后一步就会是我们要的答案，不同之处只在于中间输入，在尾递归那是从输入依次减一直到零，在循环这则是 i 从零一路加一直到初始输入值。这显然不是什么本质差别，因为这里的循环重要的只是次数，我只要把

for i in range(n)

改成

for i in range(n, 0, -1)

让 i 变成递减就可以得到与尾递归几乎一样的流程了。

而事实上他们也确实没什么区别，你再看看尾递归求阶乘的例子，把

return f(n-1, n*result)

里的第一个变量 n 拿来做循环范围，第二个变量 n*result 拿去做循环体，一个等价的循环结构就出来了。所以尾递归和循环就一步之差，尾递归的好处在于它处理对输入范围未知的情况方便点。比如你要抓取个很大的数据库，一次只能抓二十条，尾递归的话你就一直抓抓到出错为止，循环你就得先去读入整个数据库看看它总共有多少条目，算出得循环几次。

结论

结论就是这事挺好玩的，要是你也想用 HTML / CSS写点什么不妨动手试试。如果觉得程序有点复杂无处下手的话，试着先把你的程序写成循环或者尾递归的形式看看，也许思路就出来了。

致谢

今天是图灵的忌日，这篇文章献给他，感谢他带给我的快乐。

hacker emblem