公平的多样性

考虑一个预测犯人是否会再次犯罪的模型，假如我们追踪被打分的嫌犯在之后两年的表现发现：

1.那些没有再犯的白人，24%的人当初被认为会再犯，而没有再犯的黑人里45%的人当初被认为会再犯；在真的再犯的白人里，48%的人当初被认为不会再犯，在真的再犯的黑人里，28%的人当初被认为不会再犯。你觉得这个模型公平吗？如果不公平，歧视了谁？

2.如果预测会再犯的白人里59%真的再犯了，预测会再犯的黑人里63%再犯；预测不会再犯的白人里71%没有再犯，预测不会再犯的黑人里65%没有再犯。你觉得这模型公平吗？如果不公平，歧视了谁？

没什么意外的话我猜你的答案是1歧视了黑人，2还大致公平。我不在乎你的答案是否跟我一样，我在乎的是它是否跟你自己一样，因为这两个描述说的是同一个模型。

怎么会这样？让我们画几个图看看。（图重绘自 LessWrong）

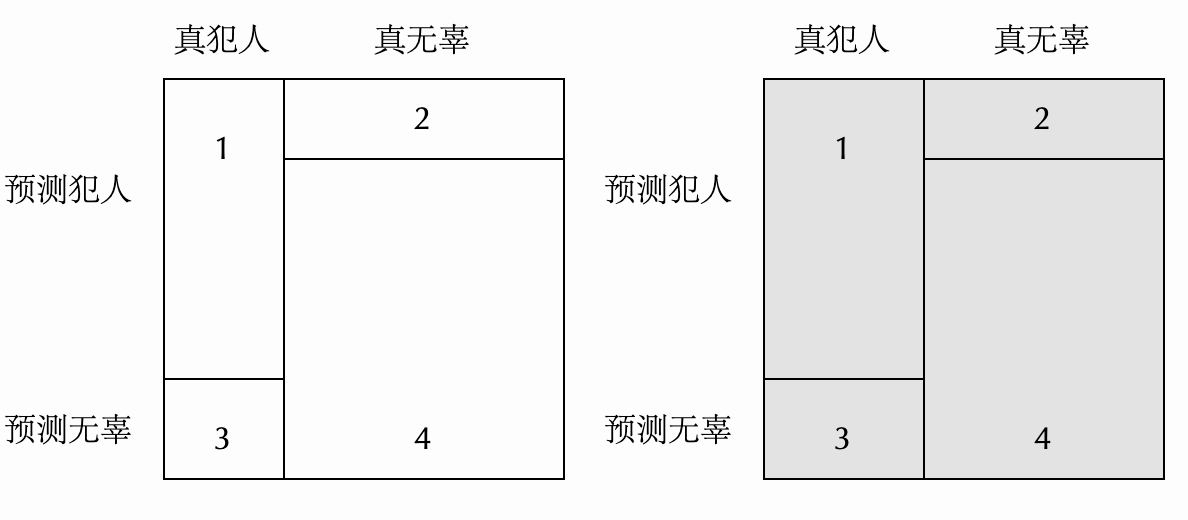
对每个正方形来说，方块1代表再犯并且模型也预测会再犯，方块2代表没有再犯但模型预测会再犯，3代表再犯但模型预测不会再犯，4代表没有再犯模型也预测不会再犯。左边的正方形代表白人，右边代表黑人，唯一的区别是出于 whatever 原因，黑人的再犯率更高，这体现在右边的方块1和3更宽。假设正方形的边长为1，则描述1里没有再犯但当初被模型预测会再犯的比例就是方块2的高度（假阳性率），再犯但当初模型预测不会再犯的比例是方块3的高度（假阴性率）。描述2里被预测会再犯的人真的再犯的比例则是方块1的面积除以方块1加2的面积（精准度/precision/positive predictive value）。现在你认为描述1里的模型是有偏见的，也就是说你认为一个公平的模型应该在不同群体上有着同样的假阳性率和假阴性率，也就是两个正方形的方块1和2应该有着相同的高度，也就是我图里画的那样。但你同时认为描述2是公平的，也就是你希望精准度在两个群体上也是相等的，能做到吗？很难，除非你的模型是100%准确之类的极端情况，否则在两个基础犯罪率不一样的群体上，假阳性率、假阳性率和精准度是不可能同时做到公平的。

在机器学习公平性研究里，假阳性率和假阴性率的公平被称作几率公平（equalized odds），假如你只关心假阳性率，也就是只在乎模型对那些无辜的人的预测，这种特例叫做机会公平（equalized opportunity），精准度的公平则叫做预测公平（predictive parity）。开头的数字并不是我编的，它们来自法院真实使用的软件 COMPAS。第一条描述的是 ProPublica 对 COMPAS 的质疑，第二条则来自 COMPAS 的自我辩护。我想说的不是“COMPAS 是对的，预测公平才是真的公平，法院没有歧视”，而是假如你没有去论证这种情境下哪个公平标准更可欲，你就不应该直接从数字上的不相等直接认定模型存在歧视。

随着 ML Fairness 这几年的快速发展，还有其他一些公平性指标也被提了出来。让我们再看一个常见的例子：银行发放贷款。（以下图片来自这篇文章，深色点代表会还贷的申请者，浅色点代表会违约的人）

机会公平：对不会违约的申请者来说，批准率是一样的。

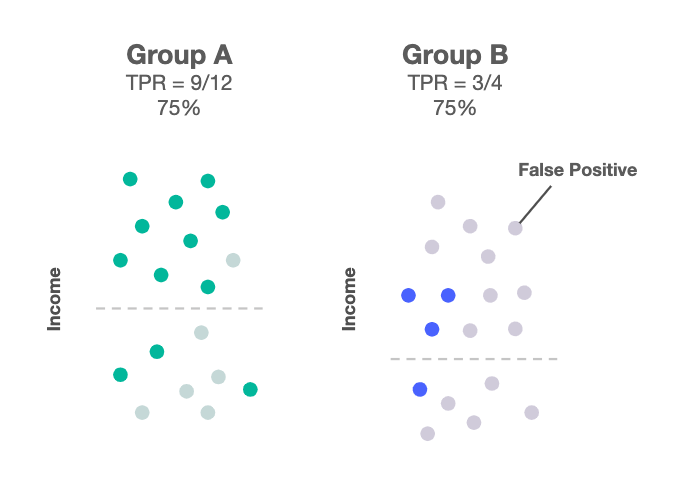
几率公平：对不会违约的申请者来说，批准率是一样的，而且对会违约的申请者来说，批准率也是一样的。

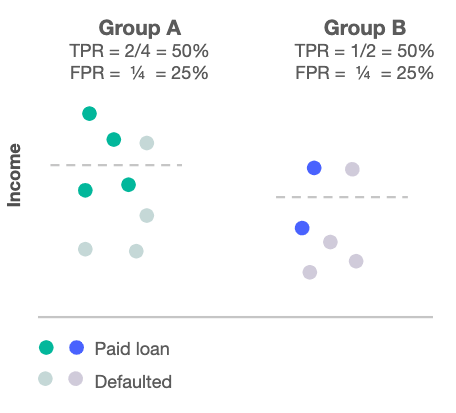
群体公平（demographic parity）：对所有申请者来说，批准率是一样的。
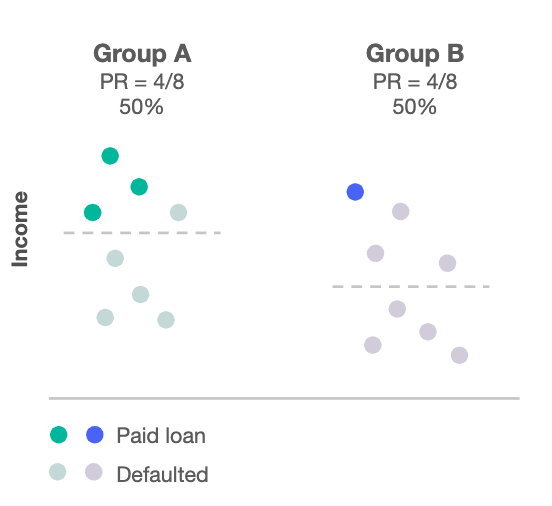
预测公平：对所有申请被批准的人来说（虚线以上的点），不同群体的违约率是一样的（虚线以上深色点和浅色点的比例一样）。那篇文章没有这个情况的图，我也懒得做，自己脑补吧。
初心公平（unawareness）：我既不歧视 A，也不歧视 B，我甚至都不在乎他们是不是人，我只在乎钱。我的目标函数里就没有种族，怎么样能赚最多的钱我就怎么做。

如果还弄不明白，玩一下 Google Research 做的这个可视化应该也就清楚了（那里的命名有点不符合主流，它的 max profit 对应这里的 unawareness，它的 group unaware 对应这里的 demographic parity）。

我们可以从这例子中学到什么？至少有这么几点吧。

1.可以证明，几率公平、群体公平和预测公平是两两互斥的，除了模型100%准确这种不现实的情况，实现其中一个则另外两个必定无法实现。

2.想想这几个目标函数，按公平性排个序；然后再看看它们产生的结果，你再排个序；然后你对比下你的两次排序，它们一样吗？如果不一样，你脑子里在想些什么？

3.即使两个群体的平均信用一样，合格/不合格申请者的平均信用一样，申请者数量一样，被批准的人里两个群体的数量依然未必一样，除非你采用的是群体公平策略。换句话说，除非你认为群体公平是唯一正确的标准，否则两个群体平均信用一样+他们贷款批准率不一样未必意味着歧视。同样的道理适用于“男女生在中学的时候平均理科分数差不多，而 MIT 理科教授却男女比例失衡，所以这一定是性别歧视”。分布很重要。

4.无论你采用哪种标准并努力去实现，都依然有可能被认为是歧视。在黑人区部署和白人区一样的警力，那没有考虑到历史造成的不平等；部署更多的警力，那是选择性执法；部署更少的警力，那是只知道保护白人社区。这种动辄得咎不动也得咎的情况和反垄断法非常相似，回想一下科斯说过的话：“我被反垄断法烦透了。假如价格涨了，法官就说是‘垄断定价’；价格跌了，就说是‘掠夺定价’；价格不变，就说是‘勾结定价’。”

最后我们考虑一个思想实验，假设现在有一个 AI，它负责在路上拦车查毒品，它一心只想尽可能地多查到毒品（初心公平），已知甲组携带毒品的概率比乙组高，请问它该怎么做？正确的做法是每次看到甲组的车都优先拦下来，因为这样最有可能发现毒品。随着甲组被针对性执法，只要他们不傻，他们就会少带毒品，但只要他们携带毒品的概率依然大于乙组，AI 就会继续针对他们，直到两组携带率一样。所以假如最终两组的携带率一样，那就说明这是个一心为公毫无私念的好 AI，否则携带率低——注意是低——的那组被歧视了，AI 应该把更多的精力花在携带率高的那组上。

与之前的例子不同，这里初心公平自动实现了预测公平（不妨称之为“后效公平”），原因也很简单，我们考虑了激励。可以理解，这种考虑激励的分析在新兴的 ML Fairness 社区还没有多少人谈论（我没准是第一个把它们联系到一块的？），但似乎没有什么明显的理由认为它不值得考虑。Again，我不是说后效公平才是真正的公平，而是你不能因为两个群体携带毒品的概率一样但被拦下来的概率不一样就觉得这说明了系统性歧视，除非你花时间去论证了后效公平为什么不成立。不然它除了说明你思考的不够全面，什么也说明不了。